图形学算法

Bresenham 算法

Bresenham 算法是计算机图形学中用于绘制直线的一种算法。 Bresenham 算法的思想是：在一条直线上，从起点到终点，每次移动一个像素，直到到达终点。

为什么要用到算法？

如果纯数学计算，需要计算出起点到终点的所有点。例如画直线，那么需要构建的直线方程，然后计算出所有点。而斜率，这样计算过程中会用到浮点数和除法。影响效率，尤其是没有FPU的CPU。

LineTo原理

一般的方法，通过y=kx+b的直线方程，直接计算点。随后将点坐标四舍五入到整数。

def draw_line(self, x0, y0, x1, y1, color="#ffffff"):
    dx = abs(x1 - x0)
    dy = abs(y1 - y0)
    sx = -1 if x0 > x1 else 1
    sy = -1 if y0 > y1 else 1
    
    k = dy/dx
    b = y0 - k*x0
    
    x = x0
    y = y0
    if dx > dy:
        cnt = dx + 1
        for i in range(cnt):
            self.draw_point(x, y, color)
            x += sx
            y = k*x + b
    else:
        cnt = dy + 1
        for i in range(cnt):
            self.draw_point(x, y, color)
            y += sy
            x = (y - b)/k

坐标系的对应关系？

假设第一象限的点为(x, y)，那么其他象限对应的点分别为：

第二象限：(-x, y)
第三象限：(-x, -y)
第四象限：(x, -y)

因此，在计算直线时，只需要考虑第一象限的点。其他象限的点，根据对称关系，可以计算出来。

往哪个方向移动？

第一象限的点，又可以做个区分：

对于k > 1的情况，向x轴正方向移动
对于k < 1的情况，向y轴正方向移动。

因为上述两种情况，关于y=x对称，因此只要计算出一个，另一个可以计算出来。比如点(x, y)，那么(y, x)即为它的对称点。当然了，也可以从其他角度来考虑，但是本质上是一样的。

这里重点重点理解 k < 1的情况：也即

假设(x0, y0)为起点，(x1, y1)为终点。用长边为dx，短边为dy。两点连线为斜边。画一个直角三角形来理解。

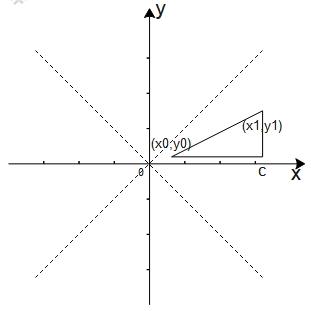
若 , 则

为了不使用浮点数，因此讲上述形式变为：

若 , 则

至于k>1的情况，直接将该直角三角形画到贴近y轴即可。那么此时，长边为dy，短边为dx。因此和上述公式原理一致。

上述原理整合

将k > 1和k < 1的情况合并，，然后根据d的正负，来决定y轴正方向移动还是x轴正方向移动。
将四个象限原理合并，用sx(sign of x)和sy 来表示需要移动的方向。例如x > 0表示向正方向移动，x < 0表示向负方向移动。

# Bresenham 算法示例：
def draw_line(x0, y0, x1, y1):
    dx = abs(x1 - x0)
    dy = abs(y1 - y0)
    sx = 1 if x0 < x1 else -1
    sy = 1 if y0 < y1 else -1

    err = dx - dy
    while True:
        draw(x0, y0)
        # 判断是否到达终点
        if x0 == x1 and y0 == y1:
            break
        
        e2 = 2 * err

        # k>1的情况
        # 这里的-dy是因为显示器左上角为原点，y轴正方向向下
        if e2 > -dy:
            # 这里本质上是 err += -dy
            err -= dy
            x0 += sx
        
        # k<1的情况
        if e2 < dx:
            err += dx
            y0 += sy

曼哈顿距离和欧几里得距离

曼哈顿距离和欧几里得距离的区别是：曼哈顿距离不考虑坐标轴的方向，而欧几里得距离考虑坐标轴的方向。

曼哈顿距离

曼哈顿距离是两个点之间的直线距离。曼哈顿距离的公式：

欧几里得距离

欧几里得距离是两点之间的直线距离。欧几里得距离的公式：

曼哈顿距离和欧几里得距离的代码实现

def manhattan_distance(p1, p2):
    return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])

def euclidean_distance(p1, p2):
    return math.sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)