数据结构

1. 简介

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。是设计和实现高效算法的基础。

数据结构的主要分类包括：

分类	说明	举例
集合	只是“同属一个集合”，元素无相互关系
线性结构	元素存在一对一的相互关系	数组、链表、栈和队列
树形结构	元素存在一对多的相互关系	二叉树、完全二叉树、二叉查找树和堆
图形结构	元素存在多对多的相互关系	有向图和无向图

常见的存储结构如下：

• 顺序存储：借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系
• 链式存储：借助指示元素存储地址的指针表示数据元素之间的逻辑关系

接口函数原型

// -------------------- 初始化 --------------------
struct* new(...);                   // 创建
void free(struct**);                // 释放

// 内部接口
// init 初始化  <构造函数>
// destory 销毁 <析构函数>

// 外部实现
int compare(void* obj1, void* obj2);// 比较函数，new后立刻配置（树、图必须）

// -------------------- 核心功能 --------------------
// 核心操作
bool push(const void* obj);         // [栈、队列] 入栈/入队
bool push_front(const void* obj);   // [双端队列] 头部入队
bool push_back(const void* obj);    // [双端队列] 尾部入队

bool pop(void* obj);                // [栈、队列] 出栈/出队
bool pop_front(void* obj);          // [双端队列] 头部出队
bool pop_back(void* obj);           // [双端队列] 尾部出队

bool peek(void* obj);               // [栈]            查看栈顶元素
bool front(void* obj);              // [队列、双端队列] 查看头部元素
bool back(void* obj);               // [队列、双端队列] 查看尾部元素

// bool insert(const void* obj);       // [树] 插入元素 <insert用于和位置相关操作>
// bool delete(const void* obj);       // [树] 删除元素

// bool add_(const void* obj);         // [图：顶点、边] 添加元素 <add不考虑位置关系>
// bool del_(const void* obj);         // [图：顶点、边] 删除元素 
// bool find_(const void* obj);        // [图：顶点、边] 查找元素

// 基础操作
uint32_t size();                    // 获取大小
bool empty();                       // 判断是否为空
bool full();                        // 判断是否为满
void clear();                       // 清空
uint32_t capacity();                // [动态数组] 获取容量

// 迭代器操作
iterator_t iter(...);               // 返回迭代器
bool iter_hasnext();                // 是否有下一个元素
void* iter_next();                  // 迭代器下一个元素

// -------------------- 扩展功能 --------------------
// 元素相关操作
bool append(const void* obj);        // 追加元素 <push_back> 一般用于list 
// bool remove(const void *obj);        // 删除元素 <暂不使用该命名>
bool find(const void* obj);          // 查找元素 <返回值，bool/uint32_t/void*待定？>
bool contains(const void* obj);      // 判断元素是否存在 <返回bool>
uint32_t count(const void* obj);     // 统计元素obj的个数

// 索引相关操作
uint32_t index(void *obj);                      // 获取元素索引
bool insert(uint32_t index, const void* obj);   // 插入元素 <非树>
bool delete(uint32_t index, void* obj);         // 删除元素
// bool erase(uint32_t index);                     // 删除元素<暂时不用该命名>
bool set(uint32_t index, const void* obj);      // 设置元素
bool get(uint32_t index, void* obj);            // 获取元素

2. 数组

• 优点 空间效率高、随机访问、
• 缺点 插入删除效率低、长度不可变、空间浪费

数组的典型应用：

• 随机访问
• 排序和搜索： 快速排序、归并排序、二分查找等
• 查找表： 字库
• 数据结构： 栈、队列、哈希表、堆、图等（图等邻接矩阵本质上是二维数组）

3. 链表

链表（Linked List）是一种常见的基础数据结构，也是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存储下一个节点的指针（Pointer），通过指针链接次序实现数据的逻辑顺序。

链表由一系列节点（链表中的元素）组成，节点可以在运行时动态生成。每个节点包括两个部分：

• 存储数据元素的数据域
• 存储下一个节点地址的指针域

分类

链表分类	说明
单链表	包含头节点和尾节点以及若干个中间节点，各节点之间通过指针链接
双链表	单链表中的引用指针具有相反的两个方向，能相互指向
循环链表	将单链表的头节点与尾节点通过指针链接起来，形成环状结构

对比

项目	数组	链表
查找
插入
删除

这里的查找指的是查找第几个元素。

【Q1】 链表的插入前，需要遍历链表，查找插入位置。那么为什么插入效率高呢？为什么不是？

【A1】 若链表的操作流程为，先查找元素再删除元素。那么时间复杂度确实是。但是链表的增删优势，在其他应用有体现。比如双向队列，插入和删除效率都为。

单链表的典型应用：

• 栈和队列
• 哈希表
• 图

双链表的典型应用：

• 高级数据结构： 红黑树、B树等的父节点
• 浏览器历史
• LRU算法

循环链表

• 时间片轮转调度算法
• 数据缓存区

链表示例

// 暂不展示，可以参考stack/queue/deque，实现原理都是类似的

4. 栈

栈（Stack）是一种特殊的数据结构，它遵循后进先出（LIFO, Last In First Out）的原则。这意味着最后一个被添加到栈中的元素将是第一个被移除的元素。栈通常用于实现函数调用、括号匹配、表达式求值等场景。

核心操作

方法	操作	说明	时间复杂度
push	压栈	添加元素到栈顶
pop	出栈	移除并返回栈顶的元素
peek	访问栈顶	返回栈顶的元素，但不移除

栈的实现可以用数组或链表来实现。使用数组时，通常会将数组的最后一个位置作为栈顶，因为数组的末尾添加和移除元素的效率最高。使用链表时，可以将链表的头部作为栈顶，这样添加和移除元素的效率也很高。

典型应用

• 程序内存管理： 调用函数

基于数组的栈

参考如下示例中的stack_new2

基于链表的栈

#ifndef _STACK_H_
#define _STACK_H_

#include "unicstl_internal.h"

struct _stack_node
{
    void * obj;
    struct _stack_node * next;
};

struct _stack
{
    // -------------------- private -------------------- 
    /**
     * @brief head pointer of stack
     * 1. linklist: head->next is valid, head->obj is NULL
     * 2. array: head->obj is valid, head->next is NULL, 
     */
    struct _stack_node * _head;
    
    uint32_t _size;
    uint32_t _obj_size;
    uint32_t _capacity;
    uint32_t _ratio;

    struct _iterator _iter;

    void (*_destory)(struct _stack* self);

    // -------------------- public -------------------- 
    // kernel
    bool (*push)(struct _stack* self, void* obj);
    bool (*pop)(struct _stack* self, void* obj);
    bool (*peek)(struct _stack* self, void* obj);
    
    // base
    uint32_t (*size)(struct _stack* self);
    uint32_t (*capacity)(struct _stack* self);
    bool (*empty)(struct _stack* self);
    bool (*clear)(struct _stack* self);
    
    // iter
    iterator_t (*iter)(struct _stack* self);

    // -------------------- debug -------------------- 
    void (*print)(struct _stack* self);
    void (*print_obj)(void* obj);
};
typedef struct _stack* stack_t;

// create and free stack
stack_t stack_new(uint32_t obj_size);
stack_t stack_new2(uint32_t obj_size, uint32_t capacity);

void stack_free(stack_t* stack);

#endif // _STACK_H_

5. 队列

队列（Queue）也是一种特殊的数据结构，它遵循先进先出（FIFO, First In First Out）的原则。这意味着第一个被添加到队列中的元素将是第一个被移除的元素。

队列通常用于实现任务调度、缓冲区管理、打印任务等场景。

核心操作

队列

方法	操作	说明
push	入队	将一个元素添加到队列的末尾
pop	出队	移除并返回队列的头部元素
front	查看队头	返回队列的头部元素，但不移除
back	查看队尾	返回队列的尾部元素，但不移除
empty	判断队空
full	判断队满

双向队列

兼顾栈和队列的特性

参考deque

方法	操作
push_front	添加到队头
push_back	添加到队尾
pop_front	移除队头元素
pop_back	移除队尾元素
front	查看队头元素
back	查看队尾元素
empty	判断队空

典型应用

• 操作系统中，进程和线程的执行顺序
• 网络通讯，缓冲区管理
• 算法中，实现各种搜索和优化问题

基于数组的队列

参考如下示例中的queue_new2

基于链表的队列

#ifndef _QUEUE_H_
#define _QUEUE_H_

#include "unicstl_internal.h"

struct _queue_node
{
    void  *obj;
    struct _queue_node * next;
};

struct _queue
{
    // -------------------- private -------------------- 
    struct _queue_node * _front;
    struct _queue_node * _back;

    uint32_t _index_front;
    uint32_t _index_back;

    uint32_t _obj_size;
    uint32_t _size;
    uint32_t _capacity;
    uint32_t _ratio;

    struct _iterator _iter;

    void (*_destory)(struct _queue* self);

    // -------------------- public -------------------- 
    // kernel
    bool (*push)(struct _queue* self, void* obj);
    bool (*pop)(struct _queue* self, void* obj);
    bool (*back)(struct _queue* self, void* obj);
    bool (*front)(struct _queue* self, void* obj);
    bool (*empty)(struct _queue* self);
    bool (*full)(struct _queue* self);

    // base
    uint32_t (*size)(struct _queue* self);
    uint32_t (*capacity)(struct _queue* self);
    bool (*clear)(struct _queue* self);

    // iter
    iterator_t (*iter)(struct _queue* self);
    
    // -------------------- debug -------------------- 
    void (*print)(struct _queue* self);
    void (*print_obj)(void* obj);
};
typedef struct _queue* queue_t;

// create and free queue
queue_t queue_new(uint32_t obj_size);
queue_t queue_new2( uint32_t obj_size, uint32_t capacity);

void queue_free(queue_t* queue);

#endif // _QUEUE_H_

基于链表的双向队列

#ifndef _DEQUE_H_
#define _DEQUE_H_

#include "unicstl_internal.h"

enum _deque_order
{
    DEQUE_FORWARD,
    DEQUE_REVERSE,
};

struct _deque_node
{
    void* obj;
    struct _deque_node* prev;
    struct _deque_node* next;
};

struct _deque
{
    // -------------------- private -------------------- 
    struct _deque_node* _head;
    struct _deque_node* _tail;

    uint32_t _obj_size;
    uint32_t _size;
    // uint32_t _capacity;
    // uint32_t _ratio;

    struct _iterator _iter;

    void (*_destory)(struct _deque* self);

    // -------------------- public -------------------- 
    // kernel
    bool (*push_back)(struct _deque* self, void* obj);
    bool (*push_front)(struct _deque* self, void* obj);
    bool (*pop_back)(struct _deque* self, void* obj);
    bool (*pop_front)(struct _deque* self, void* obj);
    bool (*back)(struct _deque* self, void* obj);
    bool (*front)(struct _deque* self, void* obj);
    
    // base
    uint32_t(*size)(struct _deque* self);
    bool (*clear)(struct _deque* self);
    bool (*empty)(struct _deque* self);

    // iter
    iterator_t (*iter)(struct _deque* self, enum _deque_order order);

    // -------------------- debug -------------------- 
    void (*print)(struct _deque* self);
    void (*print_obj)(void* obj);
};
typedef struct _deque* deque_t;

// create and free deque
deque_t deque_new(uint32_t obj_size);

void deque_free(deque_t* deque);

#endif

6. 树

树（Tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=0）个有限节点组成一个具有层次关系的集合。

相关概念	英文名	说明
根节点	root node	树中的第一个节点，没有父节点
父节点	parent node	每个节点的直接前驱节点，它的直接前驱节点有且只有一个
左子节点	left child node
右子节点	right child node
兄弟节点	sibling node	具有相同父节点的节点
左子树	left subtree	节点的左分支
右子树	right subtree	节点的右分支
叶子节点	leaf node	没有任何子节点的节点
边	edge	节点和节点之间的连接
节点的层次	level of node	从根节点到该节点的距离
节点的度	degree of node	节点的子节点个数，即节点的度。二叉树的话=0,1,2
树的深度（高度）	depth(height) of node	树上节点的最大层次

树有多种类型，包括二叉树、完全二叉树、满二叉树、平衡二叉树、AVL树、红黑树、B树、B+树、R树、2-3树、2-3-4树等。其中，二叉树是最常见和最基本的一种树形结构，它的每个节点最多有两个子节点，通常称为左子节点和右子节点。

树形结构在计算机科学中有许多应用，例如文件系统、XML和JSON解析、搜索引擎索引、数据库索引、人工智能中的决策树等。树形结构能够高效地表示具有层次关系的数据，并且在许多算法中发挥着重要作用，如二叉搜索树（BST）用于快速查找、插入和删除数据，堆（Heap）用于实现优先队列等。

总的来说，树是一种非常重要的数据结构，它具有独特的层次关系和广泛的应用场景。理解并掌握树的概念、分类、操作和应用是计算机科学和程序设计中不可或缺的一部分。

二叉树简介

二叉树（Binary Tree）是一种特殊的树形结构，它每个节点最多有两个子节点。

完全二叉树

完全二叉树（Complete Binary Tree）只有最底层的节点未被填满，且最底层节点尽量靠左填充。

满二叉树

满二叉树（Full Binary Tree）它的每个节点都有左右两个子节点，并且所有叶子节点都位于同一层。

【定义2】 一颗高度为h且有个节点的二叉树，称为满二叉树。

平衡二叉树

平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树，它的特点是每个节点的左右两个子树的高度差不超过1，并且左右两个子树都是一棵平衡二叉树。

平衡二叉树在保持平衡的条件下，查找、插入和删除操作的时间复杂度都是O(log n)，因此在实际应用中具有很高的效率。

平衡二叉树的实现有多种方法，其中最常见的包括AVL树和红黑树。

二叉树的退化

二叉树在某些情况下会退化为链表，即每个节点只有一个子节点。

应用场景

• 数据库和文件系统的索引结构
• 搜索引擎中的倒排索引

平衡二叉树并不是所有情况下都是最优的选择。在某些特定场景下，例如需要频繁进行大量数据的插入和删除操作，B树或B+树等数据结构可能更加适合。

遍历

遍历（Traversal）是指对树形结构中所有节点的访问过程。

深度优先遍历

depth-first traversal（DFS: depth-first search）是指从根节点出发，沿着树的深度遍历所有节点，然后逐层向下一层遍

遍历方式	说明
前序遍历	根节点 -> 左子树 -> 右子树
中序遍历	左子树 -> 根节点 -> 右子树
后序遍历	左子树 -> 右子树 -> 根节点

广度优先遍历

广度优先遍历（BFS: breadth-first search）是指从根节点出发，沿着树的宽度遍历所有节点。

堆

基于数组的二叉树，它通常用于实现堆。将二叉树中的节点按照层次顺序依次存储在数组中，可以方便地实现堆的插入和删除操作。

对满二叉树而言，若某节点的索引为i，则该节点的左子节点索引为2i+1，右子节点索引为2i+2 。

对完全二叉树而言，用None填充空节点之后，可以将其看作满二叉树，然后按照满二叉树的数组表示方式进行存储。

• 堆排序： 最大堆和最小堆

典型应用

• 优先队列
• 堆排序

二叉搜索树简介

二叉搜索树（Binary Search Tree）是一种特殊的二叉树，它满足以下性质：

• 每个节点的左子树中的所有节点值都小于该节点的值；
• 每个节点的右子树中的所有节点值都大于该节点的值；
• 每个节点的左子树和右子树都是二叉搜索树。

提示

二叉树不允许存在重复节点

示例

#ifndef _HEAP_H_
#define _HEAP_H_

#include "unicstl_internal.h"

typedef enum
{
    HEAP_MIN = 0, 
    HEAP_MAX = 1,
}heap_type;

struct _heap
{
    // -------------------- private -------------------- 
    void* obj;

    uint32_t _size;
    uint32_t _obj_size;
    uint32_t _capacity;
    uint32_t _ratio;

    heap_type _type;
    struct _iterator _iter;

    void (*_destory)(struct _heap* self);

    // -------------------- public -------------------- 
    // kernel
    bool (*push)(struct _heap* self, void* obj);
    bool (*pop)(struct _heap* self, void* obj);
    bool (*peek)(struct _heap* self, void* obj);

    // base
    bool (*empty)(struct _heap* self);
    uint32_t(*size)(struct _heap* self);
    bool (*clear)(struct _heap* self);

    // iter
    iterator_t (*iter)(struct _heap* self);
    
    // config
    compare_fun_t compare;      // !!! you have to implement this function
    
    // -------------------- debug -------------------- 
    void (*print)(struct _heap* self);
    void (*print_obj)(void* obj);
};
typedef struct _heap* heap_t;

// create and free heap
heap_t heap_max_new2(uint32_t obj_size, uint32_t capacity);
heap_t heap_min_new2(uint32_t obj_size, uint32_t capacity);

void heap_free(heap_t* heap);

#endif  // _HEAP_H_

AVL树

AVL树是最先发明的自平衡二叉查找树，由俄罗斯的数学家在1962年提出。它的主要特点是任何节点的两个子树的高度最大差为1，因此也被称为高度平衡树。

AVL树的每个节点都有一个平衡因子，其值等于该节点的左子树的高度减去右子树的高度。

平衡因子的值只能为-1、0或1。如果节点的平衡因子绝对值超过1，那么就需要通过旋转操作来恢复平衡。AVL树的旋转操作包括左旋、右旋和左右旋，这些操作可以确保树在插入或删除节点后仍然保持平衡。

AVL树在保持平衡的条件下，查找、插入和删除操作的时间复杂度都是O(log n)。这使得AVL树在很多需要高效查找、插入和删除操作的场景中非常有用，如数据库和文件系统的索引结构、搜索引擎中的倒排索引等。

AVL树并不适用于所有场景。比如需要频繁进行大量数据的插入和删除操作，B树或B+树等数据结构可能更加适合。

旋转的选择

下述情形，平衡因子等于该节点的左子树的高度减去右子树的高度。若平衡因子等于右子树减左子树高度，则重新考虑下述表格情况。原理都是一样的。

情形	描述	失衡节点平衡因子	子节点平衡因子	旋转
1	左偏树	>1	>=0	右旋
2	左偏树	>1	<0	先左旋后右旋
3	右偏树	<-1	<=0	左旋
4	右偏树	<-1	>0	先右旋后左旋

• 插入节点后：需要从这个节点开始，自底向上执行旋转操作，使所有失衡节点恢复平衡。
• 删除节点后：需要从这个节点开始，自顶向下执行旋转操作，使所有失衡节点恢复平衡。

特点：插入和删除操作的时间复杂度较高，需要频繁进行旋转操作。

典型应用

• 组织和存储大型数据，适用于高频查找、低频增删的场景
• 构建数据库的索引

红黑树

二叉搜索树示例

本示例中，平衡因子balance计算使用右子树高度减左子树高度，因此借助平衡因子进行判断的时候，与上述旋转略有区别。但原理还是一样的。

#ifndef _TREE_H_
#define _TREE_H_

#include "unicstl_internal.h"

#include "stack.h"
#include "queue.h"


typedef enum {
    RBT_RED,
    RBT_BLACK,
}rbt_color;

// dfs and bfs traversal order
enum _tree_order{
    ORDER_PRE,      // pre-order
    ORDER_IN,       // in-order
    ORDER_POST,     // post-order
    ORDER_BREADTH,  // breadth-first search [BFS]

    ORDER_PRE_R,    // right-first pre-order
    ORDER_IN_R,     // right-first in-order
    ORDER_POST_R,   // right-first post-order
    ORDER_BREADTH_R,// right-first breadth-first search [BFS]
};

struct _tree_node
{
    void *obj;
    struct _tree_node * left;
    struct _tree_node * right;
    struct _tree_node * parent;

    union 
    {
        int32_t balance;
        uint32_t color;
    };
};

struct _tree
{
    // -------------------- private -------------------- 
    struct _tree_node * _root;

    uint32_t _size;
    uint32_t _obj_size;
    uint32_t _capacity;
    uint32_t _ratio;

    stack_t stack;
    queue_t queue;

    struct _iterator _iter;

    bool (*_rebalance)(struct _tree* self, struct _tree_node* root);
    void (*_destory)(struct _tree* self);

    // -------------------- public -------------------- 
    // kernel
    bool (*insert)(struct _tree* self, void* obj);
    bool (*delete)(struct _tree* self, void* obj);
    uint32_t (*height)(struct _tree* self);

    // base
    bool (*clear)(struct _tree* self);
    bool (*empty)(struct _tree* self);
    uint32_t (*size)(struct _tree* self);

    // iter
    iterator_t (*iter)(struct _tree* self, enum _tree_order);

    // others
    bool (*min)(struct _tree* self, void* obj);
    bool (*max)(struct _tree* self, void* obj);

    // config 
    compare_fun_t compare;  // !!! you have to implement this function

    // -------------------- debug -------------------- 
    void (*print_obj)(void* obj);
};
typedef struct _tree* tree_t;

// create and free tree
tree_t tree_avl_new(uint32_t obj_size);
tree_t tree_rb_new(uint32_t obj_size);

void tree_free(tree_t* tree);

#endif // _TREE_H_

7. 图

图（Graph）是一种非线性数据结构，由节点（或顶点，Vertices）和边（Edges）组成。在图论、计算机科学和数学中，图被用来表示对象之间的关系。这些对象可以是任何事物，如人、城市、计算机等，而关系可以是道路、友谊、网络连接等。

图可以分为两种基本类型：有向图（Directed Graph）和无向图（Undirected Graph）。在有向图中，边有方向，表示从一个节点到另一个节点的单向关系。在无向图中，边没有方向，表示两个节点之间的双向关系。

图有许多重要的特性和应用，包括：

1. 连通性：确定图中是否存在从一个节点到另一个节点的路径。
2. 最短路径：找到两个节点之间的最短路径，常用于路由、网络流量分析等。
3. 最小生成树：在连通加权无向图中找到一棵包含所有节点的树，且所有边的权重之和最小。
4. 最大流：在有向图中找到从源节点到汇点节点的最大流量。
5. 匹配：在二分图中找到最大或最小匹配。

图论在计算机科学中有许多应用，包括：

• 社交网络分析：分析用户之间的关系、影响力等。
• 网络路由：确定数据包在网络中的最佳路径。
• 搜索引擎：用于网页之间的链接分析和排名。
• 电路设计：表示和分析电子元件之间的连接。
• 生物信息学：表示和分析基因、蛋白质等生物分子之间的关系。

实现图的数据结构通常包括邻接矩阵、邻接表等。邻接矩阵是一个二维数组，其中每个元素表示两个节点之间是否有边。邻接表则是一个数组，每个元素是一个列表，表示与该节点相邻的节点。

总的来说，图是表示和分析对象之间关系的重要工具，在计算机科学、数学、工程学等领域有着广泛的应用。

简介

• 图是由顶点的有穷非空集合和顶点之间的边的集合组成
• 通常表示为：G = <V, E)

  G表示图，V表示G图中顶点的集合，E表示图G中边的集合

• 相关数据结构的特点
  1. 线性结构——每个元素只有一个直接前驱和直接后继
  2. 树结构——数据元素（节点）间有明显的层次关系
  3. 图结构——数据元素（顶点）间具有任意的关系

相关概念

• 无向边

  • 通常用无序偶对(Vi, Vj)来表示

  例如：G=(V1,{E1}),其中顶点集合V1={A,B,C},边的集合E1={(A,B),(B,C),(B,A),(C,A)}

• 有向边 (也称之为"弧")

  • 通常使用有序对<Vi, Vj>来表示

  例如：G=(V2,{E2}),其中顶点集合V2={A,B,C},弧的集合E2={<A,B>,<B,C>,<B,A>,<C,A>}

• 简单图 （当前学的是简单图）

  不存在顶点到自身的边且同一条边不重复的出现

• 无向完全图

  任意的两个顶点都存在边

  • n个顶点的无向完全图有n*(n-1)/2条边

• 有向完全图

  任意两个顶点之间都存在方向互为相反的两条弧，

  • n个顶点的有向完全图有n*(n-1)条边

• 稀疏图

• 稠密图

• 权

  边or弧的参数

• 网

  带权的图

• 子图

  G=(V,{E}),G'=(V',{E'})。若V'是V的子集，E'是E的子集。则G'是G的子图

无向图 G=(V,{E})

• 若(v,v')属于E，则
  • v和v'互为邻接点
  • (v,v')与顶点v和v'相关联
• 顶点v的度

  和v相关联的边的数目，几位TD(v)

有向图 G=<V,{E}>

• 若弧<v, v'>属于E，则
  • 顶点v邻接到v' (注意和无向图称呼的区别)
  • 顶点v'邻接自v的弧<v, v'>与顶点v和v'相关联
• 入度
  • 以顶点v为头的弧的数据，记为ID(v)
• 出度
  • 以顶点v为尾部的弧的数据，记为OD(v)
• 度
  • v的度为 TD(v)=ID(v)+OD(v)

路径

• 从顶点v到v'的路径是一个顶点序列
• 路径的长度

  路径上的边或者弧的长度（有向图的路径也是有向的）

• 回路/环

  从第一个顶点到最后一个顶点的路径

• 简单路径

  序列中顶点不重复的路径

• 简单回路/环

  除了第一个顶点和最后一个顶点之外，其余顶点都不重复出现的回路

连通图

• 在无向图中，若从顶点v到v'有路径，则称v和v'是连通的（若有向图，则从v到v'的路径中所有边是同向的）
• 若图G中任意两个顶点都是连通的，则称G为连通图（若为有向图，则称之为强连通图）

连通分量

无向图中极大连通子图

图的存储结构

邻接矩阵

使用矩阵描述图中顶点之间的关系（及弧或者边的权值）。缺点是占用空间大

• 有向图
• 无向图

邻接表

链式存储方式，相对邻接矩阵省空间。但不方便判断两顶点间是否有边

• 无向图
• 有向图

图的遍历

从图的任意一个顶点出发，对图中所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作，图的其他算法，如求解连通性问题，拓扑排序，求关键路径等都是建立在遍历算法的基础上的。

• 图结构的复杂性导致其遍历操作的复杂性，主要体现在以下几个方面
  1. 在图结构中，没有一个自然首节点，图中任意一个顶点都可以作为首节点。
  2. 在非连通图中，从一个顶点出发，仅仅能够访问它所在的连通分量上的所有顶点。因此还需要考虑如何选取下一个出发点来访问其余的连通分量。
  3. 在图结构中，若存在回路，则一个顶点被访问之后，有可能回路返回该顶点
  4. 图结构中，一个顶点可以和其他多个顶点相连，当该顶点被访问后，需要考虑如何访问下一个顶点的问题

深度优先遍历 Depth First Search

类似于树的先序遍历

• 从图中某个顶点v开始访问，随后再访问未被访问过的邻接点，以当前邻接点作为新的起点继续访问，直到图中所有和v有路径相通的顶点都被访问到。若此时图中还存在未被访问过的顶点，则另外选择图中未曾被访问过的顶点作为起始点，重复以上流程，直到所有的顶点都被访问到为止

广度优先遍历 Breadth First Search

类似于树的按层次遍历

• 从图中某个顶点v开发访问，随后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问他们的邻接点，并使"先被访问的邻接点"先于"后被访问的顶点的邻接点"被访问(队列实现吧)，直到图中所有已被访问过的顶点的邻接点都被访问过。若此时图中还存在未被访问过的顶点，则另选择图中未曾被访问过的顶点作为起始点，重复上述过程。直到所有的顶点都被访问到为止。

BFS 适用于不断扩大范围找到最优解的情况
DFS 适用于目标比较明确，以找到目标为主的情况

图的应用

• 最小生成树

  定义：构造连通网的最小代价生成树，成为最小生成树

  1. 普利姆(Prim)算法

     对于稠密图有优势

  2. 克鲁斯卡尔(Kruskal)算法

     对于稀疏图有优势，因为Kruskal是针对边来展开的

• 最短路径

  对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，且称路径上的第一个顶点是源点，最后一个顶点是终点。

  1. 迪杰斯特拉(Dijkstra)算法
  2. 弗洛伊德(Floyd)算法

• 拓扑排序

图的示例

#ifndef _GRAPH_H
#define _GRAPH_H

#include "unicstl_internal.h"

#include "stack.h"
#include "queue.h"

enum _graph_type
{
    GRAPH_UNDIRECTED,
    GRAPH_DIRECTED,
    // GRAPH_UNDIRECTED_WEIGHT,
    // GRAPH_DIRECTED_WEIGHT,
};

enum _graph_search
{
    GRAPH_DFS,
    GRAPH_BFS,
};

struct _graph_edge
{
    uint32_t weight;
    struct _graph_edge* next;
    void *target;
};

struct _graph_node
{
    void* obj;
    struct _graph_node* next;

    bool visited;
    struct _graph_edge* edgehead;
};

struct _graph
{
    // -------------------- private -------------------- 
    struct _graph_node* _head;

    uint32_t _size;
    uint32_t _obj_size;
    uint32_t _capacity;
    uint32_t _ratio;

    enum _graph_type _type;
    enum _graph_search _search;

    stack_t stack;
    queue_t queue;

    struct _iterator _iter;

    void (*_destory)(struct _graph* self);

    // -------------------- public -------------------- 
    // kernel
    // -> vertex
    bool (*add_vertex)(struct _graph* self, void* obj);
    bool (*del_vertex)(struct _graph* self, void* obj);
    bool (*find_vertex)(struct _graph* self, void* obj);
    // -> edge
    bool (*add_edge)(struct _graph* self, void* from, void* to, uint32_t weight);
    bool (*del_edge)(struct _graph* self, void* from, void* to);
    bool (*find_edge)(struct _graph* self, void* from, void* to);

    // base
    uint32_t(*size)(struct _graph* self);
    uint32_t(*capacity)(struct _graph* self);
    bool (*empty)(struct _graph* self);
    bool (*full)(struct _graph* self);
    bool (*clear)(struct _graph* self);

    // iter
    iterator_t (*iter)(struct _graph* self, enum _graph_search search, void *obj);

    // config 
    compare_fun_t compare;  // !!! you have to implement this function

    // others
    bool (*from_matrix)(struct _graph* self, void* obj, uint32_t* edges, uint32_t size);

    // -------------------- debug -------------------- 
    void (*print)(struct _graph* self);
    void (*print_obj)(void* obj);
};
typedef struct _graph* graph_t;

graph_t graph_new(uint32_t obj_size);
// graph_t graph_new2(uint32_t obj_size, uint32_t capacity);

void graph_free(graph_t* graph);

#endif

from pydotplus import Dot, Node, Edge
import os

# 该图配置
graph = {'A': ['B', 'C', 'F'],
         'B': ['C', 'D'],
         'C': ['D'],
         'D': ['C'],
         'E': ['F', 'D'],
         'F': ['C']
         }


def dotgraph(graph):
    __graph = Dot(rankdir='TB', fontname="Fangsong",
                  fontcolor='blue', label="有向图的示例")
    __graph.set_type('digraph')
    __graph.set_name('digraph_demo')

    __graph.set_node_defaults(
        fontname="Fangsong", style='filled', fillcolor='yellow')
    __graph.set_edge_defaults(fontname="Fangsong", color='black')

    for key, value in graph.items():
        # 若节点没有特殊label或者其他属性需求
        # 可以直接以节点名称显示
        # 直接标记方向，不用手动添加
        # node = Node(key)
        # __graph.add_node(node)
        for v in value:
            edge = Edge(key, v)
            __graph.add_edge(edge)

    ret = __graph.write_raw("demo.dot")
    if ret is not True:
        print('生成demo.dot失败')
    ret = __graph.write_svg("demo.svg")
    if ret is not True:
        print('生成graph.svg失败')

    # ret = __graph.write_png("demo.png")
    # if ret is not True:
    #     print('生成graph.png失败')

    return __graph


def find_path(graph, start, end, path=[]):
    """
        在图graph中找路径：
        从顶点start到顶点end
        走过的路径为path
    """
    path = path + [start]
    # 3.0 若当找到路径尾部，则返回该路径
    if start == end:
        return path
    # 1.0 判断当前顶点是否在图内
    if start not in graph.keys():
        return None
    for node in graph[start]:
        if node not in path:
            # 2.0 以当前顶点为起点，继续找路径
            newpath = find_path(graph, node, end, path)
            # 4.0 返回该路径
            if newpath:
                return newpath
    # 这个没有什么用吗 ？
    # return path


def find_all_paths(graph, start, end, path=[], paths=[]):
    path = path + [start]
    if start == end:
        paths.append(path)
        return path
    if start not in graph.keys():
        return None
    for node in graph[start]:
        if node not in path:
            newpaths = find_all_paths(graph, node, end, path)
    if paths == []:
        return None
    return paths


def find_short_path(graph, start, end, path=[]):
    path = path + [start]
    if start == end:
        return path
    if start not in graph.keys():
        return None

    shortpath = None
    for node in graph[start]:
        if node not in path:
            newpath = find_path(graph, node, end, path)
            if newpath:
                if not shortpath or len(newpath) < len(shortpath):
                    shortpath = newpath
    return shortpath


def breadth_first_search(graph, start):
    prenodes = [start]   # 前驱节点
    travel = [start]    # 已遍历过的顶点

    graph_sets = set(graph.keys())
    travel_sets = set(travel)
    while travel_sets < graph_sets:
        # 当前驱节点未空时退出
        while prenodes:
            nextnodes = []   # 当前顶点的邻接点
            for prenode in prenodes:
                for curnode in graph[prenode]:      # 遍历当前层的节点
                    if curnode not in travel:       # 判断当前层节点是否被访问国
                        travel.append(curnode)      # 若没有被访问过，则入队
                        nextnodes.append(curnode)   # 将当前节点追加如新的前驱节点队列
            # 当前层的节点都遍历完毕，则开始下一层的遍历
            prenodes = nextnodes
        travel_sets = set(travel)
        prenodes = list(graph_sets - travel_sets)
        if prenodes != []:
            prenodes.sort()
            travel.append(prenodes[0])
    return travel


def depth_first_search(graph, start):
    travel = []
    stack = [start]

    graph_sets = set(graph.keys())
    travel_sets = set(travel)
    while travel_sets < graph_sets:
        # 堆栈空的时候退出
        while stack:
            curnode = stack.pop()           # 栈顶弹出
            if curnode not in travel:       # 判断当前节点是否已经被访问过
                travel.append(curnode)      # 若没访问过，则入队
            for nextnode in graph[curnode]: # 遍历当前节点林邻接点
                if nextnode not in travel:  # 没有被访问过的顶点全部入栈
                    stack.append(nextnode)
        travel_sets = set(travel)
        leftnode = list(graph_sets - travel_sets)
        if leftnode != []:
            leftnode.sort()
            stack.append(leftnode[0])
    return travel


if __name__ == '__main__':
    result = find_path(graph, 'A', 'D')
    print("1. 路径查找结果：", result)
    print('---------------------------------')

    result = find_all_paths(graph, 'A', 'D')
    print("2. 全路径查找结果：", result)
    print("路径个数：", len(result))
    i = 1
    for path in result:
        print('路径{0:2d}为：{1}'.format(i, path))
        i += 1
    print('---------------------------------')

    result = find_short_path(graph, 'A', 'D')
    print("3. 查找最短路径：", result)
    print('---------------------------------')

    # 生成图表
    dotgraph(graph)

    # 广度优先遍历
    result = breadth_first_search(graph, 'A')
    print(result)

    # 深度优先遍历
    result = depth_first_search(graph, 'A')
    print(result)

8. 哈希表

比如：C++的map、Python的dict、Java的HashMap等。

哈希表（hash table），也称为散列表，通过建立键 key 与值 value 之间的映射，实现高效的元素查询。映射函数也叫做散列函数，存放记录的数组叫做散列表。

哈希表的关键思想是使用哈希函数将键映射到存储桶。更确切地说，当我们插入一个新的键时，哈希函数将决定该键应该分配到哪个桶（bucket）中，并将该键存储在相应的桶中；当我们想要搜索一个键时，哈希表将使用相同的哈希函数来查找对应的桶，并只在特定的桶中进行搜索。

哈希表有两种常见的实现方式：哈希集合和哈希映射。哈希集合用于存储非重复值，而哈希映射则用于存储(key, value)键值对。

对比

项目	数组	链表	哈希表
查找
插入
删除

哈希表中进行增删查改的时间复杂度都是，非常高效。但是哈希表需要选择合适的哈希函数、处理哈希冲突以及管理扩容等。

典型应用

• ID和姓名

基于数组的哈希表

映射关系

哈希的冲突和扩容

通常情况下哈希函数的输入空间远大于输出空间，因此简单的扩容，能解决问题，但效率太低。

链式地址

Java采用链式地址，内置数组长度达到64且链表长度达到8时，链表会转化为红黑树以提神性能。

链式地址（separate chaining）将单个元素转换为链表，将键值对作为链表节点，将所有发生冲突的键值对都存储在同一链表中。

缺点： 比数组占用空间大，查询效率低。

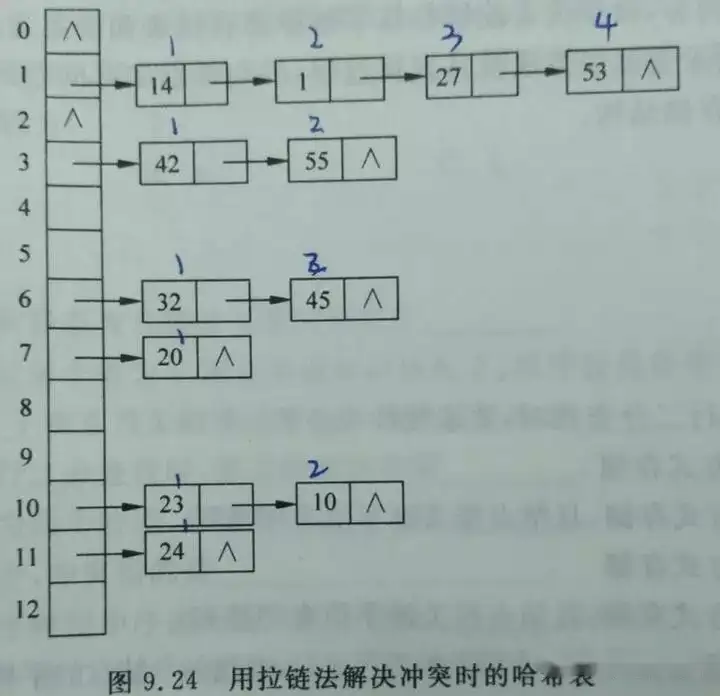
• 查询元素： 输入key，经过哈希函数计算得到index，然后遍历链表并对比key以查找目标键值对
• 添加元素： 通过哈希函数访问链表头节点，然后添加新节点。
• 删除元素： 通过哈希函数访问链表头节点，然后遍历链表，找到key对应的节点，将其删除。

开放地址

开放寻址（open addressing）不引入额外的数据结构，而是通过“多次探测”来处理哈希冲突，探测方式主要包括线性探测、平方探测和多次哈希等。

1. 线性探测

当发生冲突时，从当前位置开始，依次往后探测（步长一般为1），直到找到一个空位置。

缺点 连续的位置造成的冲突概率更大，从而进一步促使该位置的聚堆生长，行程恶性循环。最终增删查改效率下降。聚集现象

2. 平方探测

又称二次探测，和线性探测类似，但步长为平方。 优点 缓解线性探测的聚集效应，数据分布更加均匀。 缺点 仍存在聚集现象，哈希表中有空桶无法被访问到。

3. 多次哈希

若发生冲突，则使用多个哈希函数计算出多个索引，依次访问。虽然不易产生聚集，但会增加计算量。

4. 伪随机探测

线性探测和平方探测的改进，通过随机数生成器来决定步长。

9. 列表

许多编程语言中的标准库提供的列表是基于动态数组实现的，比如Python中的list、Java中的ArrayList、C++中的vector等。

如果当使用数组实现列表时，长度不可变的性质会导致列表的实用性降低。因此采用动态数组（dynamic array）来实现。

#ifndef _LIST_H_
#define _LIST_H_

#include "unicstl_internal.h"
#include "iterator.h"

#define LIST_UNLIMITED  INT32_MAX

struct _list
{
    // -------------------- private --------------------
    void *obj;

    uint32_t _obj_size;
    uint32_t _size;
    uint32_t _capacity;
    uint32_t _ratio;
    uint32_t _cur;

    struct _iterator _iter;

    void (*_destory)(struct _list *self);

    // -------------------- public --------------------
    // kernel
    bool (*append)(struct _list *self, void *obj);
    bool (*pop)(struct _list *self, void *obj);
    
    bool (*insert)(struct _list *self, int index, void *obj);
    bool (*delete)(struct _list *self, int index, void *obj);

    bool (*get)(struct _list *self, int index, void *obj);
    bool (*set)(struct _list *self, int index, void *obj);

    int (*index)(struct _list *self, void *obj);        // retval -1 if not found
    // bool (*contains)(struct _list *self, void *obj);

    // base
    uint32_t (*size)(struct _list *self);
    uint32_t (*capacity)(struct _list *self);
    bool (*empty)(struct _list *self);
    bool (*clear)(struct _list *self);

    // iter
    iterator_t (*iter)(struct _list *self);

    // others
    struct _list* (*slice)(struct _list *self, int start, int end, int step);
    // struct _list* (*copy)(struct _list *self);
    
    // config
    compare_fun_t compare;      // !!! you have to implement this function

    // -------------------- debug --------------------
    void (*print)(struct _list *self);
    void (*print_obj)(void *obj);
};
typedef struct _list *list_t;

// create and free list
list_t list_new2(uint32_t obj_size, uint32_t capacity);

void list_free(list_t *list);

#endif // _LIST_H_

10. 迭代器

迭代器是访问容器（如列表、集合、映射等）中元素的通用接口。它提供了一种统一的方式来遍历和操作容器的元素，而不需要了解底层数据结构的细节。

我目前实现的迭代器，只支持访问容器中的元素，但不支持修改（否则发生不可预料的异常，比如tree中的迭代器）。

而且tree中的迭代器可以通过tree->iter(...)获取迭代器结构体指针，方便接口统一。不同的容器，获取的迭代器的初始参数略有不同，比如tree支持前序、中序和后序、以及广度优先遍历等，deque支持双向遍历等。

迭代器示例如下

#ifndef _ITER_H_
#define _ITER_H_

#include "unicstl_internal.h"

struct _iterator
{
    // ---------- private ---------- 
    void* _container;   // pointer to stack/queue/tree ...

    void* _node;        // current node 
    uint32_t _index;    // current index
    uint32_t _order;

    // ---------- public ---------- 
    bool (*hasnext)(struct _iterator* self);
    const void* (*next)(struct _iterator* self);
};
typedef struct _iterator* iterator_t;

#endif // !_ITER_H_